A vector and its basis

Posted by Michbeck on Mai - 6 - 2015

A vector in mathematics is just a tuple of numbers. When you first come in contact with vectors maybe in school you usually deal with tuples of two numbers like $v=\begin{pmatrix}2 \\ -1\end{pmatrix} \in \mathbb{R}^2$ or with three numbers like $w=\begin{pmatrix}1 \\ -3 \\ 2\end{pmatrix} \in \mathbb{R}^3$ .

So far so good. You have vectors and you can represent them geometrically as arrows in a nice two-dimensional coordinate system. You can add them, multiply them and perform the dot product. At this point the term of a vector basis does not concern you at all.

In order to go a step further I want to focus here on the way vectors are defined in respect to a specific vector basis and how to perform a coordinate transformation to change the vector basis. We want to think of vectors here as tuples of coordinates that are always defined in respect to a certain vector basis.

So what is a vector basis? A basis for a vector space is a set of vectors that are linearly independent of each other and span this vector space. By span I mean that all other vectors in the vector space can be derived by linear combination of these basis vectors. The most basic vector basis is the standard basis $E$ . Let’s work out all examples in $\mathbb{R}^2$ here:

$E=\begin{Bmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \; \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{Bmatrix}$

So let’s assume the vector $v=\begin{pmatrix}2 \\ -1\end{pmatrix}$ is defined in respect to the standard basis. That means the tuple $\begin{pmatrix}2 \\ -1\end{pmatrix}$ represents the coordinates of $v$ in respect to the standard basis. We notate it like this:

$\begin{bmatrix}v\end{bmatrix}_{E}=\begin{pmatrix}2 \\ -1\end{pmatrix}$

This is the easy way of defining a vector by taking $E$ as the basis. You can draw a 2d coordinate system and draw an arrow from the origin to the point (2, -1) to geometrically represent vector v.
Now to show the difference we further take another vector $w$ defined in respect to the basis $B$ .

$B=\begin{Bmatrix}\begin{pmatrix}0\\1\end{pmatrix},\; \begin{pmatrix}-1\\0\end{pmatrix} \end{Bmatrix}$ , $\begin{bmatrix}w\end{bmatrix}_{B}=\begin{pmatrix}3 \\ 5\end{pmatrix}$

So this is an important step. We have a vector basis B being different from E. But hey, we have defined B in respect to the standard basis $E$ ! Why? Vectors forming a basis are just vectors and they are defined in respect to a specific vector basis like every vector is. Let’s analyse this further. Defining a vector basis always means that you create a relation towards another basis. So a basis is not defined somewhere on the green lawn but in reference to another existing basis. In this way we create a relation between vectors throughout different coordinate systems.
A straight forward way to realize this is to define a vector basis like $B$ different from the standard basis and try to draw the basis vectors of $B$ on a paper without taking the standard basis in mind as a reference for the coordinates. You can draw them in an arbitrary way. It further means that vectors themselves are not aware of the basis they are defined in respect to.

In the above example I derived B from the standard basis being rotated by 90° in counter-clock-wise order. To finally get the coordinates of the two (rotated) basis vectors I thought of what coordinates they have in respect to the standard basis.

Linear combination and basis change

Let’s go further and see how we can represent a vector by its basis. The vector basis definition says every vector can be represented by a linear combination of the basis vectors and its coordinates. For the vector v it looks like this:

$v=2\cdot\begin{pmatrix} 1 \\ 0 \end{pmatrix}+(-1)\cdot\begin{pmatrix} 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 2 \\ -1 \end{pmatrix}$

In contrast we have the linear combination for $w$ :

$w=3\cdot\begin{pmatrix}0\\1\end{pmatrix}+5\cdot\begin{pmatrix}-1\\0\end{pmatrix}=\begin{pmatrix}-5\\3\end{pmatrix}$

We notice that the linear combination for $v$ yields a resulting vector equal to $v$ . In contrast the linear combination representing $w$ yields coordinates different to the original coordinates of $w$ : $\begin{pmatrix}3\\5\end{pmatrix}\neq\begin{pmatrix}-5\\3\end{pmatrix}$ . So what happened here? We actually changed the vector basis by calculating the result of the linear combinations. The coefficients in the linear combination are the coordinates of the vector in respect to the basis the vector is defined in. For $w$ this is $\begin{bmatrix}w\end{bmatrix}_{B}=\begin{pmatrix}3 \\ 5\end{pmatrix}$ . But the result of the linear combination are the coordinates of the vector in respect to the basis where the vectors basis itself is defined in. As the two base vectors of the basis $B$ are defined in respect to the standard basis $E$ we get the coordinates of $w$ in respect to $E$ . That is $\begin{bmatrix}w\end{bmatrix}_{E}=\begin{pmatrix}-5 \\ 3\end{pmatrix}$ .
Note that we didn’t see a change of coordinates in the linear combination of vector $v$ above because $v$ is already defined in respect to the standard basis $E$ .

Well let us summarize what we observed so far. We have a vector basis $B$ formed from a set of base vectors which coordinates are defined in respect to another vector basis $B‘$ . We further have a vector $v$ and the coordinates of $v$ in respect to $B$ . If we represent $v$ by linearly combining the base vectors of $B$ we obtain the coordinates of $v$ in respect to $B‘$ . We call this vector basis change or coordinate transformation.

Let me try to explain this insight more intuitively.
We formed a basis by defining base vectors in respect to an already existing basis. So the coordinates of the base vectors tell us how we have to linearly combine the existing base vectors to derive the new base vectors. Thus the base vectors of the new basis represent the way to get from an existing basis to the new basis. For me this sounded confusing first, because considering this I would expect doing the linear combination would get my coordinates from the existing basis to the new basis. But the opposite is the case as we saw above. The reason is that every base vector of the new basis comprises the way to derive itself from the existing base vectors. And every vector defined in respect to this new basis also comprises the way how to be derived from the the new base vectors. In result we have a chain of linear combinations going from the existing basis throughout every new basis being defined in respect to just the previous basis. We just link linear combinations together. If you substitute the respective basis vectors within the linear combinations by their own linear combination from their basis vectors you will see this relation.

Invert the basis change

So far we only observed the one way ticket of vector basis change. With the above example of our vector $w$ we transformed its coordinates from the basis $B$ to the standard basis $E$ . Now the question arises how to transform the coordinates in the opposite direction?
We put two vector basis in relation to each other by defining one basis in respect to the other basis. Remember: In our example above we defined the base vectors of basis $B$ in respect to the standard basis $E$ . To transform coordinates in the opposite direction we have to create the opposite relation between the two basis. For our example we have to define the standard basis $E$ in respect to the basis $B$ . This yields two vectors again. Their coordinates are the coefficients in the linear combination with the basis vectors of $B$ .

Taking our above example we have to define the standard basis $E$ in respect to the basis $B$ . As we derived $B$ by rotating the standard basis 90° counter-clock-wise we can easily give the coordinates for both base vectors of $E$ in respect to $B$ .

$\begin{bmatrix}e_{1} \end{bmatrix}_{B}=\begin{pmatrix}0\\-1\end{pmatrix},\;\begin{bmatrix}e_{2} \end{bmatrix}_{B}=\begin{pmatrix}1\\0\end{pmatrix}$

These two vectors represent the coordinate-transformed standard basis and we denote it by $E_{B}$ .

$E_{B}=\begin{Bmatrix} \begin{pmatrix}0\\-1\end{pmatrix}, \; \begin{pmatrix}1\\0\end{pmatrix} \end{Bmatrix}$

Note that the coordinates of $w$ in respect to the standard basis $E$ given by $\begin{bmatrix}w\end{bmatrix}_{E}$ are still valid for the transformed basis $E_{B}$ as we only described this basis in respect to another basis. If we now take the coordinates of $w$ in respect to $E$ and linearly combine them with the basis $E_{B}$ we should obtain the coordinates of $w$ in respect to $B$ that we defined at the very beginning above.

$\begin{bmatrix}w\end{bmatrix}_{E_{B}}=\begin{bmatrix}w\end{bmatrix}_{E}=\begin{pmatrix}-5\\3\end{pmatrix}$
$\begin{bmatrix}w\end{bmatrix}_{B}=-5\cdot\begin{pmatrix}0\\-1\end{pmatrix}+3\cdot\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}3\\5\end{pmatrix}$

Switch to matrix notation

The linear combination we use to represent a vector through its basis can be notated more compactly by the use of a matrix. Therefore you take all base vectors of the vector basis and write them as columns into a matrix. This matrix is often denoted as the change of basis matrix. An example: We have the vector basis $B$ defined in respect to the standard basis $E$ and a vector $w$ defined in respect to $B$ .

$B=\begin{Bmatrix}\begin{pmatrix}0\\1\end{pmatrix},\; \begin{pmatrix}-1\\0\end{pmatrix} \end{Bmatrix}$ , $\begin{bmatrix}w\end{bmatrix}_{B}=\begin{pmatrix}3 \\ 5\end{pmatrix}$

The change of basis matrix $M_{B}$ would be:

$M_{B}=\begin{pmatrix}0&-1\\1&0\end{pmatrix}$

The linear combination is done as matrix multiplication by the use of $M_{B}$ .

$\begin{bmatrix}w\end{bmatrix}_{E}=\begin{pmatrix}0&-1\\1&0\end{pmatrix}\cdot\begin{bmatrix}w\end{bmatrix}_{B}$

If you put in the coordinates of $w$ in respect to $B$ from above you get:

$\begin{pmatrix}0&-1\\1&0\end{pmatrix}\cdot\begin{pmatrix}3 \\ 5\end{pmatrix}=\begin{pmatrix}-5 \\ 3\end{pmatrix}$

Note that every linear combination can be expressed by the use of such a matrix where the combined vectors are the columns of the matrix and the multiplied column vector contains the coefficients.

The matrix notation gives us a more intuitive way to invert the change of basis. Just take the inverse matrix of $M_{B}$ and multiply it with coordinates defined in vector basis $E$ .

Geometric interpretation

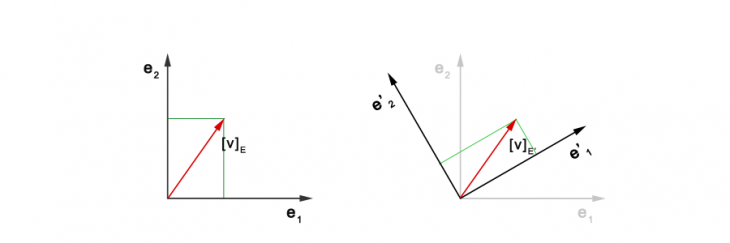
My domain is 3d computer graphics. That’s why I am always dealing with vectors as arrows in my mind. In fact you could also deal with vectors in a pure mathematical sense and just treat them as tuples defined in a linear space. But often the visual illustration of vector concerns is quite helpful to clarify things.

The image above shows a vector $v$ being defined in respect to a basis $E$ on the left side. The green lines illustrate the coordinates of $v$ in respect to the base vectors $e_{1}, e_{2}$ . On the right side we have $v$ defined in respect to a rotated basis $E‘$ . We observe how the coordinates of $v$ in respect to $E‘$ on the right side are different from its coordinates in respect to $E$ on the left side.

Note that we deal with vectors here rather than points. If we consider orthogonal vector basis only, then a vector basis change means geometrically that the standard vector basis gets rotated or scaled to derive a different basis. We cannot move the vector basis away from the origin. You can consider any vector basis to be located at the same origin.

Learn more: Video tutorial series on vector basis change.

Author: Michael Keutel | 06.05.2015

One Response so far.

Brett Anthony sagt:

5. April 2020 um 12:19 Uhr

Incredibly helpful article! Thanks for writing this! 🙂