The following techniques compute AO in object space. This space comprises all coordinate systems among the rendering pipeline defined before stage of projection: local model coordinate system, world coordinate system, camera coordinate system.
[Mill93] first published a concept being very close to Ambient Occlusion: Accessibility Shading. Tangent-spheres were used to check how accessible surface points are. Bigger tangent-spheres represent points strongly exposed to the incoming light and vice versa. He gains a shadowing of cavities and creases.
Following methods were concentrated on solving the given AO integral equation. They mostly use a common technique to solve non-analytical integrals: the Monte Carlo Integration. It utilizes statistical methods to compute an approximation of the correct solution. Basically it computes the value of the given integral for a set of choosen arguments – so called samples – and derives the approximate solution by a weighted avarage of the resulting sample values. The higher the number of samples, the closer we get to the correct solution of the integral. A higher sample count of course implicates increasing computation time. A very good introduction to the monte carlo technique is given by Robin Green in his „Spherical Harmonic Lighting: The Gritty Details„.
In use of monte carlo integration the first AO approaches were based on raytracing . Rays (sample rays), originating at the respective surface point, were shot throughout the visible hemisphere and tested for intersection with scene geometry. This concept is also called inside-out-approach. Raytracing is usually not feasible for realtime rendering, why this approach was mainly used for offline rendering in film productions etc. In this context [Lan02] introduced the notion of AO as a part of ambient environments.
[Pha04] implement raytracing in a preprocessing step and bake the given occlusion values into a texture for later use in realtime shading. This approach is limited to rigid geometry and non-animated scenes.
Further an outside-in-method employing the graphics hardware is presented. They invert the problem and compute the avarage visibility of a surface point from the viewpoint of sampling light sources. Therefore lightsources are placed at sample positions on the visible hemisphere and the respective shadow map is computed to give the visibility information. Intuitively a point being always in shadow is entirely occluded by geometry while an point exposed to light is visible from all sample positions.
[Sat04] present a simliar approach, based on an outside-in-technique. They utilize the OpenGL Extension ARB_OCCLUSION_QUERY to gain the visibility information of surface points.
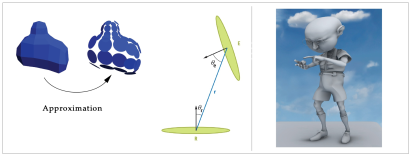
A first flexible approach feasible for animated scenes is given by [Bun05]. The scene geometry is approximated by oriented discs, created at every vertex. Theses discs are able to occlude each other while the amount of occlusion is computed by with the respective projected solid angle. As the approximation of geometry is dependent on the scene complexity, this method might suffer from a very poor performance for mass data scenarios. Additionally it reveals artefacts for low tesselated objects, due to the linear interpolation of occlusion values between vertices. Hoberock and Jia refine this approach and eliminate artefacts (Link: http://http.developer.nvidia.com/GPUGems3/gpugems3_ch12.html).
Other techniques focus on approximation of scene geometry by spherical proxys, in order to compute occlusion more effective. [Heg06] use spheres to approximate trees and render natural scenes of vegetation with an ambient occlusion efffect. [Slo07] utilize Precomputed Radiance Transfer to compute occlusion of spherical proxys. [Kon05] rely on spherical segments in a preprocessing step and save their occlusion-parameters in so called Ambient Occlusion Fields.
Summary
The approaches referenced here mostly suffer from expensive preprocessing steps, complex datastructures, artefacts due to approximation or bad performance because of the dependence on scene complexity.
A more effectie alternative for AO computation is given by methods operating entirely in screen space.
References
[Bun05] M. Bunnel. Dynamic ambient occlusion and indirect lighting. Gpu gems 2: programming techniques for high-performance graphics and general-purpose computation, pages 223-234, 2005. (Link: http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter14.html)
[Heg06] K. Hegeman, S. Premoze, M. Ashikhmin, and G. Drettakis. Approximate ambient occlusion for trees. In I3D 06: Proceedings of the 2006 symposium on Interactive 3D graphics and games, pages 87-92, New York, NY, USA, 2006. ACM. ISBN 1-59593-295-X.
[Kon05] J. Kontkanen and S. Laine. Ambient occlusion fields. In Proceedings of ACM SIGGRAPH 2005 Symposium on Interactive 3D Graphics and Games, pages 41-48. ACM Press, 2005.
[Lan02] Landis, H. Production-Ready Global Illumination, ACM SIGGRPAH 2002 courses, 2002.
[Pha04] S. Pharr, Matt Green. Ambient occlusion. GPU Gems: Programming Techniques, Tips and Tricks for Real-Time Graphics, 2004. (Link: http://http.developer.nvidia.com/GPUGems/gpugems_ch17.html)
[Sat04] M. Sattler, R. Sarlette, G. Zachmann, and R. Klein. Hardware-accelerated ambient occlusion computation. In Vision, Modeling, and Visualization, pages 331-338, 2004.
[Slo07] P.-P. Sloan, N. K. Govindaraju, D. Nowrouzezahrai, and J. Snyder. Image-based proxy accumulation for real-time soft global illumination. In PG07: Proceedings of the 15th Pacific Conference on Computer Graphics and Applications, pages 97-105, Washington, DC, USA, 2007. IEEE Computer Society. ISBN 0-7695-3009-5. doi: http://dx.doi.org/10.1109/PG.2007.35