This article is intended to cover the basic idea and definition of Ambient Occlusion.

SSAO - vector based approach: Gouraud Shading (left), AO (middle), composite result (right). (Sibenik Cathedral is courtesy of Marko Dabrovic, Dragon is courtesy of Stanford University)

What is Ambient Occlusion – Definition

Ambient Occlusion (AO) is a global illumination effect regarding the occlusion of surface points by surrounding scene-geometry. In general interreflections of diffuse light cause an indirect illumination of every surface point within a 3d-scene. AO computes how a surface point is actually exposed to this indirect diffuse light. The reader may be reminded that all possible directions of incoming light, illuminating a point, are described by a hemisphere centered around the normal of the respective point. Thus AO declares the brightness of a surface point to be functionally dependent on the amount of surrounding geometry occluding its visible hemisphere. The following figure illustrates this concept:

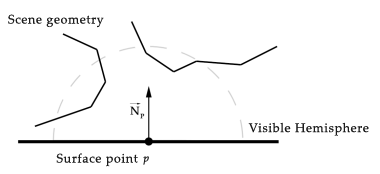
Concept of Ambient Occlusion with P being the surface point of interest and N its surface normal. P is shadowed as its visible hemisphere is partly covered by geometry.

CG scenes illuminated with Ambient Occlusion often look similar to real world scenes under an overcast sky. The reason is a strong dispersion of the sunlight caused by the dense clouds. As a result, light is extremely diffuse and objects are lit from nearly all directions what is the AO assumption again. This lighting conditions constrain the human perception of shape from shading and human visual system has to gain essential depth cues from soft shadows in cavities and creases [Lan99]. As AO simulates these shadows, human visual system can acquire essential clues of depth, curvature and spatial arrangement from this global illumination effect.

Current research sometimes distinguishes high and low frequency occlusion. High frequency occlusion is caused on very detailed surfaces, where a lot of small faces occlude each other while low frequency occlusion can be observed as big soft shadowing caused by distant large occluders.

Mathematical definition and computation of AO

The following equation is the standard mathematical definition of ambient occlusion concerning all directions of incoming light within the visible hemisphere.

Computation of Ambient Occlusion by solving an integral over the visible hemisphere

The occlusion function, equation (2), has to be solved for every solid angle within Omega. Additionally a cosine-weight is expressed by the attached dot product. This is based on [Lan02] who applies Lamberts law on the concept of ambient occlusion and concludes that the occlusion is maximal for surface points along the direction of the normal.

The integral can not be solved analytically. This is a problem often occuring in CG equations, as most of them are declared by the integral over the visible hemisphere. Here we face the problem that equation (2) cannot be integrated like an analytic function. Its value can only be determined by checking every single direction within the hemisphere for interesection with scene geometry and thus detecting an occlusion. As this solution is computationally unacceptable, research has been concentrated on approximative solutions to the AO-equation. (see articles: Ambient Occlusion – approaches in object space, Ambient Occlusion – approaches in screen space (SSAO) )

Equation (2) could also be declared inversely: 1 if p is unoccluded in the respective direction etc. This would represent an accessibilty function rather than an occlusion function and is equivalent to changing A(p) to 1 – A(p). That can be handled as recquired. It just determines how the final modification of the brightness of the surface point has to be done.

References

[Lan02] Landis, H. Production-Ready Global Illumination, ACM SIGGRPAH 2002 courses, 2002.

[Lan99] Langer, M.S., Bülthoff, H.H. Perception of shape from shading on a cloudy day, Max-Planck-Institut für biologische Kybernetik, 1999.