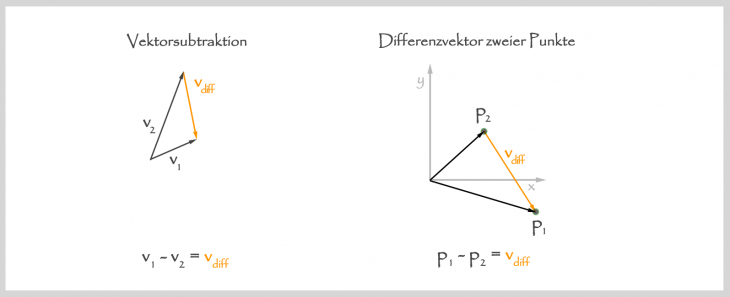
Wenn ich mit Vektoren arbeite und diese voneinander subtrahiere stellt sich mir immer wieder die Frage: In welcher Reihenfolge muss ich zwei Vektoren subtrahieren, so dass der Ergebnisvektor in die gewünschte Richtung zeigt? Es geht also um die geometrische Interpretation der Subtraktion.
Da die Vektorsubtraktion für jede einzelne Koordinate des Vektors einfach nur eine gewöhnliche Subtraktion von Zahlen darstellt lässt sich eine einfache Regel ableiten. Eine normale Subtraktion zweier Zahlen besteht aus dem Minuend (der verringert wird) und dem Subtrahent (der vom Minuend abgezogen wird), also Minuend – Subtrahent = Differenzwert. Beispiel: . Umgekehrt kann man sagen: Addiert man den Differenzwert auf den Subtrahent erhält man genau wieder den Minuend. Ich drücke es für mich auch gern anders aus: Der Differenzwert zeigt additiv mit dem Subtrahent zum Minuend, also entgegen der Lesrichtung der Subtraktion. Übertrage ich diese Regel auf die Subtraktion von Vektoren so zeigt der Ergebnisvektor stets von rechts nach links, vom Subtrahent zum Minuend. Geometrisch bedeutet die Subtraktion, dass zwei Vektoren (
,
) in den gleichen Anfangspunkt gelegt werden und man erhält denjenigen Vektor (
) der die Spitzen beider Vektoren verbindet. Aufgrund der oben erklärten Regel zeigt
für
stets von
zu
. Ich merke mir ganz einfach, dass der Ergebnis entgegen der Lesrichtung der Differenz zeigt.
Was für Vektoren gilt, gilt hier auch für Punkte. Vektoren repräsentieren eine Verschiebung in einem bestimmten Raum und sind nicht von einem Koordinatenursprung abhängig. Sie fliegen quasi frei im Raum :). Punkte stellen hingegen feste Koordinaten in einem Koordinatensystem mit Ursprung dar. Man kann z.Bsp. Vektoren zu Punkten addieren um diese zu verschieben. Ebenso kann man den Differenzvektor zwischen zwei Punkten berechnen, der die Verschiebung eines Punktes zum anderen repräsentiert (siehe Affiner Raum). Die mathematische Notation für die Differenz zweier Punkte (,
) ist äquivalent zur Notation einer Vektorsubtraktion:
. Man kann sowohl
als auch
als Ortsvektor zu dem jeweiligen Punkt betrachten, womit der Term äquivalent zur Vektorsubtraktion ist. Der Ergebnisvektor
zeigt wieder von
zu
.
Autor: Michael Keutel | 20.11.2015