Rotation matrices and vector basis change

Posted by Michbeck on Mai - 4 - 2015

When you deal with 3d computer graphics you become familiar with rotation matrices and how to use them in order to rotate points in space. I want to give a short straight forward summary of rotation matrices regarding vector basis change.

The motivation for this article was the problem of rotating an object around global axis versus rotating it around local axis. To understand the involved matrices I found it useful to clarify what a rotation matrix actually does.

The common standard matrices for rotations around X, Y, Z axis rotate a point around the respective world axis. Let’s take the simple rotation matrix $R$ in $\mathbb{R}^{2}$ which rotates around an angle $\alpha$ around the imaginary z-axis. We show examples here in $\mathbb{R}^{2}$ for simplicity, but what we observe here is also valid in $\mathbb{R}^{3}$ or even $\mathbb{R}^{n}$ .

$R= \begin{pmatrix} \cos\,\alpha & -\sin\,\alpha \\ \sin\,\alpha & \cos\,\alpha \end{pmatrix}$

In order to rotate a vector $v \in \mathbb{R}^2$ you usually multiply $R$ by $v$ notated as column vector:

$\begin{pmatrix} \cos\,\alpha & -\sin\,\alpha \\ \sin\,\alpha & \cos\,\alpha \end{pmatrix}\cdot\begin{pmatrix} v_{x} \\ v_{y} \end{pmatrix}=\begin{pmatrix} v'_{x} \\ v'_{y} \end{pmatrix}$ .

Constructing a rotation matrix

Let us analyse how the matrix $R$ is constructed. $R$ is a so called change of basis matrix. It represents a vector basis being rotated in respect to the standard basis. You can derive it in two steps:

Derive the rotated coordinates of both base vectors of the standard basis in $\mathbb{R}^2$
Write the coordinates of each rotated base vector as a column vector into a matrix.

The standard basis in $\mathbb{R}^2$ is defined by:

$E=\begin{Bmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \; \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{Bmatrix}$

The coordinates of both base vectors being rotated depend on the rotation angle:

$\begin{pmatrix}1\\0\end{pmatrix}\mapsto\begin{pmatrix}\cos\alpha\\ \sin\alpha\end{pmatrix}, \;\begin{pmatrix}0\\1\end{pmatrix}\mapsto\begin{pmatrix}-\sin\alpha\\ \cos\alpha\end{pmatrix}$

The two image vectors form our rotated basis and are taken as column vectors to form our final rotation matrix $R$ :

$R= \begin{pmatrix} \cos\,\alpha & -\sin\,\alpha \\ \sin\,\alpha & \cos\,\alpha \end{pmatrix}$

So, constructing a rotation matrix is a straight forward task. We observed that a rotation matrix represents a vector basis and contains the mapped base vectors in its columns. You can find more information on vector basis and transformations between them here.

Active rotation vs. vector basis change

Like every change of basis matrix a rotation matrix transforms the coordinates of a multiplied vector $v$ from its rotated basis to the basis itself has been defined in respect to. Consider this matrix multiplication:

$R\cdot v=\begin{pmatrix} \cos\,\alpha & -\sin\,\alpha \\ \sin\,\alpha & \cos\,\alpha \end{pmatrix}\cdot\begin{pmatrix} v_{x} \\ v_{y} \end{pmatrix}=\begin{pmatrix} v'_{x} \\ v'_{y} \end{pmatrix}$

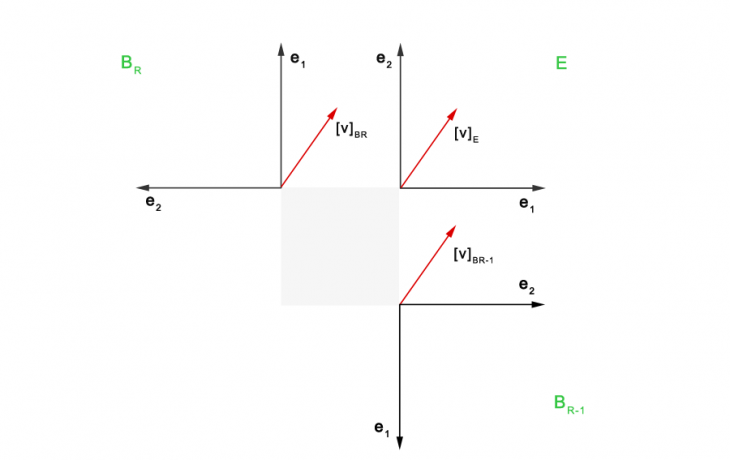
The usual way to interpret this term means to interpret the rotation as an active task: The rotation matrix rotates the given vector $v$ by some angle and gives us the transformed coordinates of $v$ denoted by $v‘$ . In contrast we see that we can interpret this term as a change of vector basis. To analyse this we explicitly define the vector basis here that is represented by the rotation matrix. Therefore we just put both base vectors into a set:

$B_{R}=\begin{Bmatrix} \begin{pmatrix} \cos\alpha \\ \sin\alpha \end{pmatrix}, \; \begin{pmatrix} -\sin\alpha \\ \cos\alpha \end{pmatrix} \end{Bmatrix}$

Actually the matrix multiplication performs a linear combination of the base vectors of $B_{R}$ and the coordinates of $v$ . This linear combination transforms the coordinates of $v$ from $B_{R}$ to the standard basis $E$ . This is already explained in detail in vector basis change. We notate it like this:

$R\cdot\begin{bmatrix}v\end{bmatrix}_{B_{R}}=\begin{bmatrix}v\end{bmatrix}_{E}$

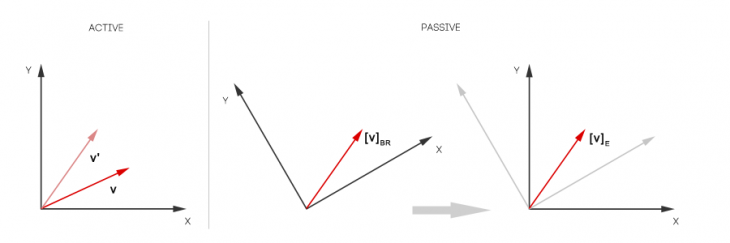
The strange thing for me is here that we assume $v$ to be defined in respect to $B_{R}$ rather than the standard basis first and in the end the rotation finally yields $v$ in respect to the standard basis. The following image illustrates this subject.

The active side shows the usual rotation interpretation. The passive side clarifies the vector basis change notion in two steps. You see how $v$ is first assumed to be defined in respect to the rotated basis $B_{R}$ . You can observe that this step rotates $v$ in the same way the basis $B_{R}$ is rotated in respect to the standard basis. The second step does the basis change and transforms the coordinates of $v$ from basis $B_{R}$ to the standard basis $E$ .

In literature you will often find active transformations versus passive transformations. Passive transformations are described as transformations on the coordinate system (basis) rather than the vector itself. Thus active and passive transformations are always inversely related to each other. Either you rotate a vector by 90° or you rotate the basis by -90° to have the same resulting vector coordinates. The vector basis change we observe here is a quite similar interpretation to a passive transformation. The passive side of the illustration above might also express a rotation of the coordinate system inversely to the rotation we actually wanted to apply on our vector. I think this is the more geometric notion for the passive interpretation. Changing the vector basis instead is a more mathematical way of thinking.

Inverting vector basis change

So far we applied the straight forward constructed rotation matrix $R$ . Every rotation has an inverse counter part that performs a rotation by the negated angle. Let us analyse the invers rotation regarding the vector basis change we observed in the preceeding sections. First we recall some properties of rotation matrices:

rotation matrices are square matrices
rotation matrices are orthogonal matrices
rotation matrices represent a orthonormal basis

From property 1. and 2. we know that the inverse of a rotation matrix is derived by transposing the rotation matrix. This is quite comfortable for 3d applications as transposing a matrix is much cheaper than inverting it. We consider here a vector basis $B_{R}$ of $\mathbb{R}^{2}$ that is derived from the standard basis $E$ being rotated by 90° in counter clock wise direction:

$B_{R}=\begin{Bmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix}, \; \begin{pmatrix} -1 \\ 0 \end{pmatrix} \end{Bmatrix}$

We know from the preceeding sections that if we put both base vectors as column vectors into a matrix we have yet constructed a rotation matrix that rotates a vector by 90° in counter clock wise direction. From this matrix we can easily derive its inverse by transposing it.

$R= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$ , $R^{-1}= \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$

In terms of vector basis change the matrix $R$ transforms a vectors coordinates from basis $B_{R}$ to basis $E$ . Matrix $R^{-1}$ intuitively goes the opposite direction. It transforms a vectors coordinates from $E$ to $B_{R}$ . Why?
Let us notate the vector basis represented by $R^{-1}$ :

$B_{R^{-1}}=\begin{Bmatrix} \begin{pmatrix} 0 \\ -1 \end{pmatrix}, \; \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{Bmatrix}$

This is a basis derived from the standard basis being rotated by -90° (clock wise direction). Represented by the matrix $R^{-1}$ this basis above all does a change of basis from $B_{R^{-1}}$ to the standard basis $E$ . But this coordinate transformation is equal to the one from $E$ to $B_{R}$ . The reason is that the relation of $B_{R^{-1}}$ to the standard basis $E$ is equal to the relation of $E$ to $B_{R}$ .

To summarize this, we observed that in order to transform coordinates into a given vector basis we need the inverse of its change of basis matrix. For rotation matrices we generate the inverse by transposing the matrix.

Author: Michael Keutel | 06.05.2015

4 Responses so far.

Vadims sagt:

21. Februar 2016 um 10:38 Uhr

Useful article! Thank you, really!
Olga sagt:

13. Juni 2017 um 10:44 Uhr

Thanks a lot, Michael! Your article helped me understand the idea of active and passive rotations.
Hank Gurdjieff sagt:

28. Juli 2019 um 22:01 Uhr

Thank you for posting this, this is very helpful. Please consider changing the font styling so users can instead font size. It’s very hard to read on mobile. I can zoom in, but then have to scroll right and left a bunch. When the website follows browser fint settings the text reflows instead. It might not look quite as nice, but it’s much more accessible. Thank you.
naksh sagt:

11. Juli 2021 um 16:16 Uhr

amazing article. thanks